In mathematics and computer science, graph theory is the study of graphs, which are mathematical structures used to model pairwise relations between objects. A graph in this context is made up of vertices, nodes, or points which are connected by edges, arcs, or lines. A graph may be undirected, meaning that there is no distinction between the two vertices associated with each edge, or its edges may be directed from one vertex to another; see Graph (discrete mathematics)for more detailed definitions and for other variations in the types of graph that are commonly considered. Graphs are one of the prime objects of study in discrete mathematics.
Graph theory is also used to study molecules in chemistry and physics. In condensed matter physics, the three-dimensional structure of complicated simulated atomic structures can be studied quantitatively by gathering statistics on graph-theoretic properties related to the topology of the atoms. In chemistry a graph makes a natural model for a molecule, where vertices represent atoms and edges bonds. This approach is especially used in computer processing of molecular structures, ranging from chemical editors to database searching. In statistical physics, graphs can represent local connections between interacting parts of a system, as well as the dynamics of a physical process on such systems. Similarly, in computational neuroscience graphs can be used to represent functional connections between brain areas that interact to give rise to various cognitive processes, where the vertices represent different areas of the brain and the edges represent the connections between those areas. Graphs are also used to represent the micro-scale channels of porous media, in which the vertices represent the pores and the edges represent the smaller channels connecting the pores.
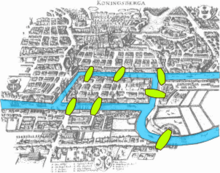
The paper written by Leonhard Euler on the Seven Bridges of Königsberg and published in 1736 is regarded as the first paper in the history of graph theory. This paper, as well as the one written byVandermonde on the knight problem, carried on with the analysis situs initiated by Leibniz. Euler's formula relating the number of edges, vertices, and faces of a convex polyhedron was studied and generalized by Cauchy and L'Huillier, and represents the beginning of the branch of mathematics known as topology.




More than one century after Euler's paper on the bridges of Königsberg and while Listing was introducing the concept of topology, Cayley was led by an interest in particular analytical forms arising from differential calculus to study a particular class of graphs, the trees. This study had many implications for theoretical chemistry. The techniques he used mainly concern the enumeration of graphs with particular properties. Enumerative graph theory then arose from the results of Cayley and the fundamental results published by Pólya between 1935 and 1937. These were generalized by De Bruijn in 1959. Cayley linked his results on trees with contemporary studies of chemical composition. The fusion of ideas from mathematics with those from chemistry began what has become part of the standard terminology of graph theory.
In particular, the term "graph" was introduced by Sylvester in a paper published in 1878 in Nature, where he draws an analogy between "quantic invariants" and "co-variants" of algebra and molecular diagrams:
- "[…] Every invariant and co-variant thus becomes expressible by a graphprecisely identical with a Kekuléan diagram or chemicograph. […] I give a rule for the geometrical multiplication of graphs, i.e. for constructing a graph to the product of in- or co-variants whose separate graphs are given. […]" (italics as in the original).
The first textbook on graph theory was written by Dénes Kőnig, and published in 1936. Another book by Frank Harary, published in 1969, was "considered the world over to be the definitive textbook on the subject", and enabled mathematicians, chemists, electrical engineers and social scientists to talk to each other. Harary donated all of the royalties to fund the Pólya Prize.

Johann Benedict Listing (25 July 1808 – 24 December 1882) was a German mathematician.


Further reading:

I was diagnosed as HEPATITIS B carrier in 2013 with fibrosis of the
ReplyDeleteliver already present. I started on antiviral medications which
reduced the viral load initially. After a couple of years the virus
became resistant. I started on HEPATITIS B Herbal treatment from
ULTIMATE LIFE CLINIC (www.ultimatelifeclinic.com) in March, 2020. Their
treatment totally reversed the virus. I did another blood test after
the 6 months long treatment and tested negative to the virus. Amazing
treatment! This treatment is a breakthrough for all HBV carriers.